Los números racionales y los irracionales.

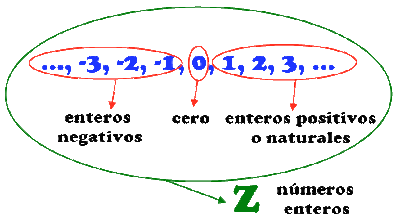
Hemos dedicado una entrada anterior a los números naturales y los enteros:

Los números naturales y los enteros

Ahora pretendemos aclarar los que se entiende por número racional y por número irracional.

Como sabemos, los números naturales surgieron de la necesidad de contar y ordenar objetos. Pero también fue necesario realizar medidas, y no todas las medidas se podían representar por cantidades enteras. De ahí surgió la idea de fracción.

La primera gran civilización que utilizó las fracciones fue la egipcia, pero solo usaban fracciones con numerador igual a 1.  

El resto de fracciones se expresaban como suma de fracciones con numerador unitario. Así, por ejemplo:

Nuestra notación habitual para designar fracciones fue introducida en Europa por Fibonacci en el siglo XIII.

A principios del siglo XV se generalizó el uso de los números decimales, pero hasta el siglo XVII no se expresaban como les conocemos hoy, separando la parte entera de la decimal con una coma o con un punto.

- Pero, ¿qué es un número racional?

Un número racional es aquel que puede expresarse en forma de fracción (es decir, como cociente de dos números enteros con denominador distinto de 0).

Observa que en la definición decimos "que puede expresarse en forma de fracción", y no "que venga expresado necesariamente en forma de fracción" . Por lo tanto, no debemos confundir los números racionales con las fracciones.

Dentro de los números racionales se incluyen muchos números que no son fracciones, pero que se pueden expresar como fracciones. Así, son números racionales:

• Los números enteros:  Por ejemplo, el 7, puesto que

• Los números decimales finitos:  Por ejemplo, 0'045, ya que

• Los números decimales infinitos periódicos (puros o mixtos):

    

El conjunto de los números racionales se representa con la letra Q, que es la inicial de la palabra "quotient" (cociente, en inglés)

-  Y entonces, ¿cuáles son los números irracionales?

Pues, como su propio nombre nos indica, son los números no racionales, es decir, los números que no pueden expresarse en forma de fracción. 

Por lo tanto, los números irracionales son los números decimales con infinitas cifras decimales no periódicas.

Ya en el siglo VII a.C. los griegos descubrieron las magnitudes irracionales al comparar la diagonal y el lado de un cuadrado o la diagonal y el lado de un pentágono regular.

Llamaron "irracionales" a estas magnitudes porque su existencia "no entraba dentro de su conocimiento racional".

Así fueron surgiendo algunos números irracionales muy conocidos:

• El "número áureo o número phi", al comparar la diagonal de cualquier pentágono regular con su lado.

• El número "raíz cuadrada de 2", al hallar la diagonal de un cuadrado de lado 1 unidad.

• El famoso "número pi", al comparar la longitud de una circunferencia con su diámetro.

Veamos algunos ejemplos de irracionales:

El conjunto de todos los números irracionales se representa con la letra I.

Ahora, fíjate en algunos irracionales muy conocidos:

• Por último, tenemos el conjunto R de los números reales que está formado por todos los números racionales y por todos los irracionales:

R = Q U I

Espero que ahora comprendas mejor esos esquemas que suelen aparecer en los libros de texto, explicándonos los distintos conjuntos numéricos. Aquí te dejo uno de ellos:

Podríamos decir que en el conjunto de los números reales están incluidos todos los números que necesitamos para realizar nuestros cálculos (todos los números que, para nosotros, "existen"...) pero aún hay varios problemas que no somos capaces de resolver con este enorme conjunto numérico:

• No podemos dividir entre cero.

• No podemos calcular raíces cuadradas de números negativos, por lo que no sabemos resolver ciertas ecuaciones de segundo grado que parecen muy elementales.

Para resolver estos problemas tendremos que introducir otros conceptos como son la noción de infinito y el conjunto de números complejos, pero eso ya es otra historia...

Os dejo unos enlaces en los que podéis encontrar vídeos que muestran algunas curiosidades de los números irracionales. Espero que os gusten:

EL NÚMERO DE ORO. LA DIVINA PROPORCIÓN

EL NÚMERO "PI"

FIBONACCI

Resolviendo ecuaciones de segundo grado.

En una entrada anterior analizamos el procedimiento para resolver las ecuaciones de primer grado. Ahora pretendemos hacerlo con las ecuaciones de segundo grado.

Se dice que una ecuación es de segundo grado cuando, después de realizar las operaciones indicadas, puede reducirse a una expresión del tipo:

donde a, b y c representan números conocidos.

Observa que el coeficiente "a" no puede ser 0 puesto que, en ese caso, la ecuación no sería de segundo grado.

Sin embargo, los coeficientes "b" y "c" sí pueden ser 0. En dicho caso, la ecuación se llama incompleta.

• Fórmula general para resolver cualquier ecuación de segundo grado (completa o incompleta):

Como seguramente habrás estudiado en clase o habrás visto en libros u otros materiales de consulta, la fórmula general para resolver cualquier ecuación de segundo grado es la siguiente:

Es muy importante que identifiques correctamente los coeficientes a, b y c en la ecuación de segundo grado para poder aplicar adecuadamente la fórmula anterior. Fíjate en los siguientes ejemplos:

Veamos ahora un ejemplo completo que ilustra el procedimiento para resolver una ecuación de segundo grado usando la fórmula general:

Ej.)  Resolver la ecuación:

- 1º Paso: Trasponer todos los términos a uno de los miembros de la igualdad y reducir términos del mismo grado (también llamados "términos semejantes"):

-  2º Paso: Dividir los dos miembros de la ecuación entre 2 para simplificar los coeficientes (Este paso es opcional):

-  3º Paso: Identificar los coeficientes  a = 1, b = -7 y c = 12, y, a continuación, aplicar la fórmula general:

• Pero, ¿cuántas soluciones puede tener una ecuación de segundo grado?

Depende de la expresión que aparece en el radicando de la fórmula general anterior, que se llama discriminante precisamente porque sirve para distinguir el número de soluciones de la ecuación de segundo grado:

Veamos, a continuación, varios ejemplos concretos:

• Técnicas específicas para resolver ecuaciones de segundo grado incompletas:

Aunque la fórmula anterior sirve para resolver cualquier ecuación de segundo grado, cuando la ecuación es incompleta se recomienda emplear alguna técnica específica que facilita su resolución.

Las recordamos en el siguiente esquema:

Observa que:

• Si  b = 0 , la técnica consiste en despejar x.
• Si  c = 0 , la técnica consiste en sacar factor común la x que se repite en los dos sumandos del primer miembro de la ecuación.

Veamos algunos ejemplos concretos:

- - - - - - - -

Al principio de esta entrada hemos visto la fórmula general para resolver ecuaciones de segundo grado pero no hemos comentado nada sobre cómo se obtiene dicha fórmula. Es muy probable que en clase tampoco te lo hayan explicado. 

Al final, por falta de tiempo, los profesores nos conformamos con que la uséis adecuadamente. Pero también es muy interesante seguir el proceso necesario para su obtención.  

La demostración que te indico a continuación se basa en "completar cuadrados" para así poder despejar fácilmente la incógnita:

- - - - - - - -

Espero haberte aclarado un poco las ideas, pero ahora debes practicar mucho porque, al fin y al cabo, el procedimiento para resolver ecuaciones es mecánico y se basa en la repetición de unos pasos y la utilización adecuada de una fórmula o de unas técnicas muy concretas.

Te indico algunos enlaces con los que podrás acceder a páginas con ejercicios resueltos sobre ecuaciones de segundo grado:

Página de VITUTOR

Página de MATEMÁTICASONLINE

Repaso del tema: PROYECTO EDUCAREX

Los números naturales y los enteros.

Desde muy temprana edad se introducen los números en nuestra vida. Ya en la educación infantil se trabaja el concepto de cantidad y los niños empiezan a familiarizarse con los símbolos 1, 2, 3... asociados al número de objetos que hay en un conjunto.

A medida que vamos creciendo aprendemos más y más números, y vamos conociendo otros conjuntos numéricos, algunos de ellos muy extraños, como los números "negativos", las "fracciones", los números "decimales"...

En esta entrada y en otras posteriores, pretendo poner un poquito de orden dentro del inmenso conjunto de números con los que hemos tenido que trabajar, aclarando algunas ideas básicas.

• Los números naturales.

Los números naturales surgen de la necesidad del hombre de contar los objetos que hay en su entorno. Su origen se remonta a la era primitiva, aunque entonces, lógicamente, no utilizaban los símbolos que actualmente conocemos.

En un principio, se supone que para contar harían marcas en los árboles, utilizarían piedras o harían nudos en las cuerdas... 

Con el paso del tiempo, empezaron a utilizar símbolos, como, por ejemplo, en el sistema de numeración romano, el egipcio, el griego, el maya...

El sistema de numeración tal y como lo conocemos en la actualidad es el indo-arábigo, y fue bastante posterior.

Los números naturales son, pues, los que se utilizan para contar y ordenar. 

Así, decimos, por ejemplo, "tengo quince años (15)" o "vivo en el tercer piso (3)"...

• El número cero.

La historia del número 0 es diferente. El hombre primitivo no tenía necesidad de contar conjuntos que no tuvieran ningún elemento. 

Para qué contar "cero" elefantes, por ejemplo; si no había ningún elefante, no había necesidad de contar nada... Por eso, el número "cero" tardó mucho tiempo en aparecer.

Aunque algunas civilizaciones ya usaron la idea de número cero representando el "vacío", este número no tuvo especial trascendencia hasta que los árabes lo exportaron a occidente desde la India. Fíjate que civilizaciones tan importantes como la romana nunca utilizaron el número cero.

Después de muchos debates, actualmente se reconoce el número cero como número natural, y, de hecho, habrás estudiado que el conjunto de los números naturales se simboliza por N (inicial de la palabra "natural") y está formado por los números:

Con los números naturales se pueden definir algunas operaciones, como la suma o la multiplicación, pero no se pueden definir otras, como la resta o la división, porque, en general, no se pueden efectuar:

• Los números enteros.

Los números negativos se llamaron inicialmente "números deudos" o "números absurdos". Aunque las primeras manifestaciones de su uso se remontan al siglo V en oriente, hasta el siglo XVI no llegan a occidente. 

Parece ser que la diferenciación entre números positivos y negativos se interpretó como créditos y débitos ("lo que tengo" y "lo que debo")

Hasta finales del siglo XVIII los números enteros no fueron aceptados universalmente.

Actualmente, utilizamos los números enteros con mucha naturalidad, por ejemplo:

• Cuando queremos distinguir entre tener 1000 euros en el banco (1000 o +1000) o deber 1000 euros al banco (-1000)

• Para diferenciar entre temperaturas sobre cero (15º C) y temperaturas bajo cero (- 2º C)

• Cuando estamos en un ascensor y queremos distinguir entre subir al tercer piso (pulsar el 3º) o bajar el garaje (pulsar el -1)...

Como sabrás, el conjunto de los números enteros está formado por los números naturales (positivos) y por los opuestos de los números naturales (negativos).

Se simboliza por la letra Z, que proviene de la expresión Zahien, que, en alemán, significa "número". 

Con los números enteros podemos seguir realizando las operaciones de sumar y multiplicar, como ocurría con los números naturales, pero ya podemos definir la resta de enteros, no así la división. 

Como sabes, los números enteros se representan en una recta del siguiente modo:

Este tipo de representación permite ordenar los números enteros sabiendo que su valor aumenta de izquierda a derecha, es decir, un número es mayor que otro cuando está representado a su derecha:

- - - - - - - - - -

Por ahora, tenemos bastante...

En una próxima entrada hablaremos de los números racionales y de los irracionales.

Y para acabar, con un poco de humor matemático...

Primeros pasos en trigonometría.

En esta entrada pretendo introducirte en el increíble mundo de la trigonometría, que, por desgracia, suele ser una parte de las matemáticas que no goza de muchas simpatías entre los alumnos, seguramente porque se han dedicado a estudiarla aprendiéndose de memoria las innumerables fórmulas que aparecen en los libros de texto, y así, desde luego, la trigonometría resulta muy aburrida.

No quiero que sea un curso acelerado de trigonometría, solo vamos a dar los primeros pasos para entender las nociones básicas y las aplicaciones prácticas que tiene.

En posteriores entradas iremos ampliando nuestros conocimientos sobre el tema.

- - - - - - - - - - -

• La palabra "trigonometría" proviene del griego y significa "medida de triángulos". Por lo tanto, la trigonometría es la parte de las matemáticas que se dedica a estudiar las relaciones entre los elementos de un triángulo (sus 3 lados y sus 3 ángulos)

Ya desde antiguo, los estudiosos de la geometría observaron que en los triángulos rectángulos semejantes la razón entre las longitudes de dos de sus lados se mantenía constante. Y lo utilizaron, entre otras cosas, para hallar medidas inaccesibles:

Si dibujamos un ángulo agudo "alfa" y trazamos varias perpendiculares a uno de los lados, formamos varios triángulos rectángulos semejantes, como se observa en la figura:

Observa que la razón (cociente) entre los lados AB y OA es igual que la razón entre A'B' y OA', y la misma también que la razón entre A''B'' y OA''. Lo mismo ocurre si dividimos cualquier otra pareja de lados correspondientes en dos de dichos triángulos. 

Por lo tanto, el resultado de dichas razones (cocientes) solo depende del ángulo considerado y no del triángulo rectángulo que tomemos. 

Decidieron, pues, poner nombre a cada una de las razones entre los lados de un triángulo rectángulo. De ahí surgieron las definiciones de seno, coseno y tangente de un ángulo agudo:

• Como puedes apreciar en las definiciones anteriores, las razones trigonométricas de ángulos agudos son cocientes entre longitudes, por lo tanto son NÚMEROS POSITIVOS (sin unidad de medida).

¡¡ Ojo !!  Todo esto cambiará cuando pasemos a trabajar con ángulos cualesquiera. Lo dicho anteriormente, solo sirve para ángulos agudos.

• Por otra parte, es muy importante que comprendas que las razones trigonométricas son números asociados a cada ángulo, por lo que es imprescindible que no olvides indicar el ángulo en cada razón trigonométrica. No tiene sentido, pues, escribir "sen", "cos" o "tg" si no indicamos a su derecha el ángulo de que estamos hallando las razones trigonométricas.

Es una "falta de ortografía matemática" escribir expresiones como:  

Supongo que estarás pensando: "Pero qué más da, si se entiende bien lo que quiero decir..." 

No da igual, tienes que esforzarte en expresar adecuadamente lo que dices porque siempre debemos hablar y escribir de forma correcta, incluso cuando usamos lenguaje matemático.

- - - - - - - - -

• Utilizando las definiciones anteriores y algunos recursos básicos de geometría (el teorema de Pitágoras y la propiedad, conocida por todos, que asegura que la suma de los tres ángulos de un triángulo es 180 grados), podemos hallar la medida de todos los elementos de un triángulo rectángulo conociendo tres de ellos (recuerda que uno de los ángulos es conocido porque es recto).

- - - - - - - - - -

¿Y qué interés práctico puede tener todo esto?

Lo curioso es que esos números (seno, coseno y tangente de un ángulo) que, de momento, no parecen tener ninguna utilidad, nos van a ayudar a resolver innumerables problemas en el futuro.

En contra de los que muchos estudiantes piensan, la trigonometría tiene muchísimas aplicaciones prácticas en campos tan diversos como pueden ser la geometría, física, arquitectura, ingeniería, cartografía, navegación, topografía, geografía, astronomía, meteorología, economía...

Es una herramienta muy útil que nos ayuda a resolver problemas como, por ejemplo:

• La obtención de la inclinación de una recta, por ejemplo, una carretera  (geometría o topografía):

• El cálculo de distancias de difícil acceso (topografía):

• El estudio de los planos inclinados en física:

• El estudio de los movimientos de ondas como la luz, el sonido o las ondas magnéticas (física):

• Determinación de modelos de temperatura o la estimación del techo de la nube (meteorología):

• La obtención de las coordenadas geográficas de un punto de la Tierra (geografía):

• La utilización de los sistemas de navegación por satélite:

• El uso de instrumentos como el GPS, por ejemplo:

• El cálculo de la distancia entre estrellas y otros cuerpos celestes (astronomía):

• La obtención de ángulos en el cielo (astronomía):

• Cálculo de distancias y fuerzas en arquitectura:

• Estudio del comportamiento cíclico de los mercados  y de la economía:

• Y otras aplicaciones que puedes encontrar si tienes interés y dedicas un rato a buscar en internet...

En la siguiente imagen se resumen algunas de las aplicaciones que hemos mencionado anteriormente:

- - - - - - - - - - -

Como ves, solo hemos dado unas pinceladas sobre el tema. Únicamente hemos definido las tres razones trigonométricas básicas y hemos visto algunas de las muchas aplicaciones del tema.

Ojalá haya conseguido motivarte para que cuando tengas que estudiar la trigonometría en clase lo hagas con ilusión puesto que es muy probable que tengas que utilizar estos recursos con frecuencia en el futuro. 

- - - - - - - - - - -

Si quieres profundizar en el tema puedes trabajar con los materiales que encontrarás en los siguientes enlaces:

MATEX: Trigonometría (1º parte)

MATEX: Trigonometría (2º parte)