Resolviendo ecuaciones de primer grado.

Parece increíble que alumnos de cursos avanzados sean capaces de plantear ejercicios en los que intervienen contenidos relativamente complicados y se equivoquen a la hora de resolver la ecuación planteada, y resulta mucho más increíble cuando, a veces, se trata de una simple ecuación de primer grado.

Lo mismo ocurre cuando hablamos con profesores de otras materias (Física, Química, Tecnología...). Suelen quejarse amargamente de que sus alumnos no saben despejar una incógnita. 

Seguramente, en su momento el profesor de matemáticas se molestó en explicar a los alumnos, paso a paso, el procedimiento que deben seguir para resolver una ecuación de primer grado, pero éstos, al final,  se quedaron con el "truco" sin comprender el por qué, y claro, con el tiempo la memoria falla y donde decíamos "...se pasa restando..." ahora recordamos "...se pasa multiplicando o dividiendo o qué se yo...". 
Como dicen algunos alumnos: "Total, ¡qué más da!, el caso es despejar la x, ¿no?... "

Es cierto, el objetivo es despejar la incógnita en un miembro de la igualdad, pero no de cualquier manera.

La idea fundamental es que una ecuación es una igualdad entre dos expresiones algebraicas, y que, por tanto, las transformaciones que realicemos para despejar la incógnita deben mantener dicha igualdad.

Esta idea se puede comprender bien si interpretamos la ecuación con una balanza que está en equilibrio.

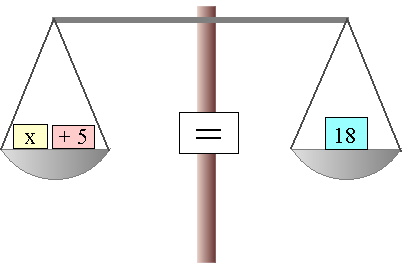
¿Qué ocurre con una balanza en equilibrio si añadimos el mismo peso en ambos platos? ¿Seguirá en equilibrio?

¿Y si quitamos de ambos platos el mismo peso?

¿Y si duplicamos o triplicamos el peso de cada plato?

¿Y si reducimos a la mitad el peso de ambos platos?

La respuesta a todas estas cuestiones es que la balanza sigue equilibrada puesto que hemos realizado las mismas transformaciones en ambos platos a la vez.

Trasladando estas reflexiones a las ecuaciones surgen las transformaciones que realizamos para resolver una ecuación de primer grado:

- Regla de la suma: Podemos sumar (o restar) a ambos miembros de una igualdad el mismo número y la igualdad sigue siendo cierta.

- Regla del producto: Podemos multiplicar (o dividir) ambos miembros de una igualdad por el mismo número (distinto de 0) y la igualdad sigue siendo cierta.

A continuación, os muestro un ejemplo de cómo se puede resolver una ecuación sencilla de primer grado, paso a paso, y su equivalencia en la balanza:

También os dejo el enlace con un vídeo que he encontrado en el que se muestra de una manera muy ilustrativa cómo se resuelven ecuaciones de primer grado mediante el método de la balanza. Por cierto, quiero agradecer a sus creadores el trabajo realizado. Espero que os guste.

Vídeo con ejemplos ilustrativos

- - - - - - - -

Confío en que, a partir de ahora, cuando dudes en si debes pasar un número al otro miembro sumando o restando, multiplicando o dividiendo... te acuerdes de la balanza y comprendas por qué el profesor te dice que "lo que está restando pasa al otro miembro sumando", o "lo que está multiplicando pasa al otro miembro dividiendo...". 

Son frases poco adecuadas porque dan la impresión de que los números saltan de un miembro a otro de la igualdad de forma caprichosa y, como acabamos de ver, no es cierto.

Estas frases solo pretenden que mecanices de una forma rápida las transformaciones que hemos visto en los ejemplos anteriores, pero muchas veces, por querer ir más rápido, haces las cosas mal ya que no entiendes lo que realmente estás haciendo.

Ante cualquier duda, piensa siempre que tienes que realizar la misma transformación en cada miembro de la igualdad para mantener el equilibrio de la balanza.

- - - - - - - -

Por último, te dejo un enlace con la página web de VITUTOR en la que encontrarás una colección de ejercicios para que practiques la resolución de ecuaciones de primer grado con la ventaja de que cuenta con la resolución completa de cada una de ellas. Espero que te sea útil.

Ejercicios para practicar