Uno de los conceptos más importantes de las matemáticas modernas es el de FUNCIÓN. Como ya hemos dedicado una entrada anterior a explicar este concepto, te dejo el enlace por si necesitas revisarlo:
Ahora pretendo que conozcas algunas aplicaciones de las funciones a situaciones de la vida cotidiana, para que comprendas la importancia que tiene este tema en tu formación.
Las funciones determinan las relaciones que existen entre distintas magnitudes tanto en Matemáticas, como en Física, Química, Medicina, Estadística, Economía, Ingeniería, Psicología... y permiten, entre otras muchas cosas, poder calcular los valores de cada una de ellas en función de otras de las que depende.
Los principales tipos de funciones son:
Los principales tipos de funciones son:
- Funciones lineales.
- Funciones cuadráticas.
- Funciones racionales. La función de proporcionalidad inversa.
- Funciones exponenciales.
- Funciones logarítmicas.
- Funciones trigonométricas.
Dedicaremos este artículo a los tres primeros tipos de funciones, y trataremos los otros tres tipos en un artículo posterior.
- - - - - - - - - - - - - - -
1. LAS FUNCIONES LINEALES
Son las funciones polinómicas de primer grado.
La representación gráfica será una recta cuya
pendiente nos informa de la rapidez de la variación de
una magnitud con respecto a la otra y la ordenada en
el origen nos informa sobre las condiciones iniciales.
Un caso particular de funciones lineales son funciones de proporcionalidad en las que las magnitudes que se relacionan son directamente proporcionales.
Por ejemplo, en economía decimos que "el precio de una compra es directamente proporcional al número de unidades compradas de un cierto producto", por lo tanto la función que relaciona ambas magnitudes es una función de proporcionalidad.
Un caso particular de funciones lineales son funciones de proporcionalidad en las que las magnitudes que se relacionan son directamente proporcionales.
Por ejemplo, en economía decimos que "el precio de una compra es directamente proporcional al número de unidades compradas de un cierto producto", por lo tanto la función que relaciona ambas magnitudes es una función de proporcionalidad.
Veamos este otro ejemplo: "El precio de la factura de la luz depende de una cantidad fija (alquiler del contador...) más una cantidad variable que es proporcional al consumo efectuado". En este caso, la relación entre el consumo efectuado y el coste de la factura viene dado por una función afín (también considerada como el caso general de función lineal)
En economía hay dos funciones que tienen especial trascendencia, como son la función de la oferta y la función de la demanda, que se consideran lineales y son las dos funciones que determinan el equilibrio de mercado.
En física se estudia el movimiento rectilíneo uniforme (MRU) en el cual, la posición de un móvil en función del tiempo viene dada mediante funciones lineales.
En la ciencia en general se utilizan con mucha frecuencia, por ejemplo, para hallar tasas de variación (por ejemplo, en el cálculo de velocidades o en el estudio de reacciones químicas).
También se usan para efectuar cambios de unidades de medida (por ejemplo, pasar de kilómetros a millas, o de grados centígrados a grados Fahrenhein) y para realizar predicciones siempre que la relación entre las variables sea aproximadamente lineal.
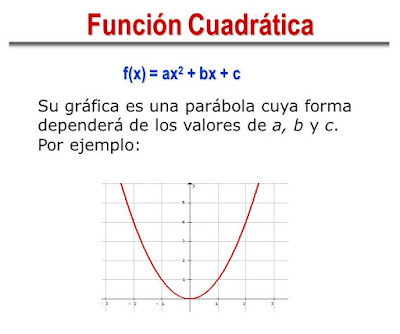
2. LAS FUNCIONES CUADRÁTICAS
Son las funciones polinómicas de segundo grado.
Se usan con mucha frecuencia en la ciencia, los negocios y la ingeniería.
En el ámbito científico, la parábola puede describir trayectorias de chorros de agua en una fuente o el botar de una pelota, y otras muchas situaciones físicas en las que interviene la gravedad.
En física, permite estudiar con precisión el tiro parabólico (por ejemplo, la trayectoria de un proyectil, la trayectoria de un balón lanzado a canasta...) y los movimientos uniformemente acelerados (MUA)
En economía, las funciones cuadráticas ayudan a predecir ganancias y pérdidas en los negocios, y determinar los valores máximos y mínimos puesto que en muchas ocasiones la función "ingresos" sigue un modelo cuadrático.
En ingeniería civil, se usan las funciones cuadráticas en la construcción de muchos edificios, puentes...
3. LAS FUNCIONES RACIONALES
Son aquellas funciones cuya expresión analítica viene dada por un cociente de polinomios.
Las más sencillas son las funciones de proporcionalidad inversa, que relacionan dos variables que son inversamente proporcionales.
La función de proporcionalidad inversa aparece en numerosos fenómenos físicos y sociales. Algunos casos comunes ilustrativos de la aplicación de este tipo de funciones serían:
- La relación entre el caudal de un grifo y el tiempo que tarda en llenar un depósito de una capacidad determinada.
- La relación entre el número de pacientes que asiste a una consulta médica de horario limitado y el tiempo que puede dedicar el médico a cada paciente.
- La relación entre la intensidad de corriente y la resistencia eléctrica en una porción de circuito sometida a una diferencia de potencial constante, conocida como ley de Ohm: V = I x R . La intensidad y la resistencia son magnitudes inversamente proporcionales.
- La relación entre la presión y el volumen en un gas ideal sometido a una temperatura constante k, que sigue el principio conocido como ley de Boyle-Mariotte: P x V = k.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados obtenidos en otras funciones más complejas ya que son simples de calcular pero permiten expresar una mayor variedad de comportamientos.
Espero que, después de mostrarte las numerosas aplicaciones de estos tipos de funciones, las estudies con más interés.
Pero ahí no acaba todo, si quieres conocer aplicaciones de las funciones exponenciales, logarítmicas y trigonométricas a la vida real solo tienes que pulsar en el siguiente enlace:
- - - - - - - - -
Pero ahí no acaba todo, si quieres conocer aplicaciones de las funciones exponenciales, logarítmicas y trigonométricas a la vida real solo tienes que pulsar en el siguiente enlace:











excelente y muy bonito
ResponderEliminarMuchas gracias. Me alegro de que te haya gustado.
EliminarGracias por la información, me a servido para una tarea y a causado que me interece más por las matemáticas!
ResponderEliminarGracias por tu comentario. Me alegro de haber colaborado a aumentar tu interés por las matemáticas.
Eliminarbuah estuvo super chidoris esa info compadre,me sirvio para sacar matricula de honor, me gusta el choriso pamplona
ResponderEliminarTu si eres pato enrique
Eliminarcoño Enrique
EliminarEnrique?
Eliminarme encanto para mi ensayo urgente era de tarea y nomas tenia un dia para hacerlo xdxd
ResponderEliminarme parece muy interesante, muchas gracias
ResponderEliminarnahhh solamente copio para la tarea xque a mi nunca me gustaran las matematicas
ResponderEliminarLo leo todo y no lo voy a negar me pareció interesante los usos múltiples a las funciones
ResponderEliminarmuy interesante toda la informaciòn muy especifica y talvez me ayude para decidirme si ser profesora de matematicas♥
ResponderEliminarBruh
ResponderEliminarse saco se un aprieto pana , gracias
ResponderEliminarme saco de un aprieto
ResponderEliminarMe salvaste para mi tarea, jaja muchas gracias.!
ResponderEliminaralguien sabe donde podemos ver dichas funciones en la psicología?
ResponderEliminarGracias por tu ayuda bro, te mereces el cielo
ResponderEliminarMuchas gracias!!!
ResponderEliminarMe ayudaron mucho para mi deber, me encantó todo y súper explicado.
Saludos a mis compañeros de 10mo B, de parte de su castroso favorito
ResponderEliminarMessirve 😎👍
ResponderEliminarExcelente explicación, se veían tan complicadas las gráficas y usted lo explica tan perfecto que uno se interesa más en las matematicas
ResponderEliminarMuchas gracias por tu comentario.
ResponderEliminarMe alegra saber que mi blog contribuye a aumentar el interés por las matemáticas. Esa fue mi intención al crearlo.
Wow
ResponderEliminarQ fáciles han sido no comprendía y gracias a este blog ya lo entendi
Me alegro de haberte ayudado a entender las matemáticas. Ese es el objetivo de este blog.
ResponderEliminarEs maravilloso el trabajo. Gracias ;P
ResponderEliminarGracias a tí por visitar mi blog
ResponderEliminarMe sirvio de mucho, gracias
ResponderEliminarGracias a tí por visitar mi blog
ResponderEliminarPerfecto! Justo lo que necesitaba.
ResponderEliminar👍👌
ResponderEliminarMuchas gracias por el tfabajo
ResponderEliminarGracias a vosotros por visitar mi blog. Me encanta saber que puede ayudar a aumentar el interés por las matemáticas
ResponderEliminarGracias x la info
ResponderEliminarMuy buena
ResponderEliminarayuda banda como desactivo el modo creativo
ResponderEliminarEste comentario ha sido eliminado por el autor.
EliminarMuy interesante👍
ResponderEliminarBuenardopolis 👌
ResponderEliminarMuchas gracias!! Me ayudo a realizar mi trabajo por la facilidad de las explicacion. Me motiva a practicar las matemáticas,ya no me dan terror.
ResponderEliminarMe alegro mucho de que te haya servido de ayuda. Cuando se entienden, las matemáticas pueden resultar apasionantes.
EliminarSúper útil está información, gracias 🤗
ResponderEliminarMe encanto.. Muy buenas explicación
ResponderEliminarMuchas gracias por vuestros comentarios
ResponderEliminarMuy buena información, porque toda la información que pone te ayuda en las materias ya que son temas principales y sabes como aplicarlo día tras día y se te hace mas fácil.
ResponderEliminar